Ⅰ. 서 론
유인비행체 가상훈련 시뮬레이터(manned flight virtual training simulator)는 유인항공기에서 발생할 수 있는 가상의 환경과 상황을 제공하여 훈련자에게 실제와 유사한 훈련 효과를 제공하는 장비이다. 이러한 시뮬레이터를 통한 공간정위상실 훈련의 효과를 극대화하기 위해 기존의 6축 스튜어트 플랫폼 구동시스템과 더불어 360deg 무한 회전을 하는 턴테이블을 포함하여야 한다.
따라서 6축 스튜어트 플렛폼(이하 ‘모션’)의 제한적 한계를 일부 극복하고 롤각과 피치각이 제어명령 값으로 유지된 상태로 헤딩각의 변화에 따른 조종사의 공간정위상실의 반응을 연구하고자 본 시스템을 개발하였다.
턴테이블 상부에 모션시스템을 장착한 것과는 달리 모션시스템 상부에 적용된 턴테이블의 경우, 턴테이블의 방향에 따라 상부에 장착된 모의조종석의 자세변화를 유지하기 위해서는 모션시스템제어명령의 회전변환을 통하여 명령을 최종적으로 계산하여야 한다.
본 논문에서는 이러한 연구주제의 실현과 실 비행 상태와는 다른 공간정위상실을 불러 일으킬 수 있는 모션시스템의 큐잉 알고리즘 개발과 그 과정에서 도출된 개발비용 절감을 위한 기술적 노하우를 전하고자 한다.
Ⅱ. 본 론
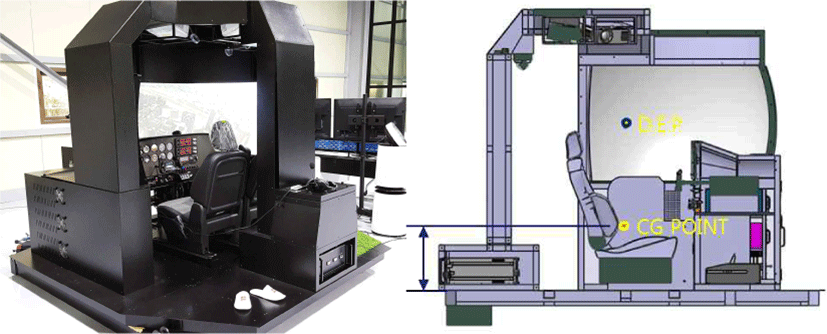
적용하고자 하는 시뮬레이터는 국토교통부의 ‘공간정보기반 실감형 콘텐츠 융복합 및 혼합현실제공 기술개발 사업’을 통해 개발된 유인비행체 가상훈련 시뮬레이터 시제작품이며, 2인 좌석을 갖춘 단발 프로펠러기의 조종석과 운동특성을 모의한 시뮬레이터이다. 적용 시뮬레이터의 사양 및 형상은 Table 1 및 Fig. 1과 같다.
| 구분 | 내용 | 비고 |
|---|---|---|
| 모의 항공기 | 단발형 프로펠러기 | C172 |
| 탑승 인원 | 2명 | 좌/우 |
| 영상 F.O.V. | 210 × 45도 | 수평, 수직 |
| 스크린 및 채널수 | 실린더형 / 3채널 | |
| 조종실 중량 | 1.5톤 | 탑승자 포함 |
| 모의 장비 | ADF, VOR, ILS, 통신 |
본 연구에 적용한 모션시스템은 (주)젠스템에서 제작한 7축 모션으로(Z6-600-2000, Fig. 2) 6축 모션의 상부 플레이트에 턴테이블을 적용하여 주문 생산하였다. Payload는 턴테이블 구조물을 포함 2ton이며, 스트로크가 최대 600mm인 Parker사의 eth80 실린더에 LS산전 서보모터를 적용한 엑츄에이터를 6-axis-stewart-platform 형태로 제작한 모델이다. Table 2는 해당 모델의 구동 사양이며, Addition Yaw는 스튜어트 플랫폼의 YAW축 구동 제한을 넘어 360도 무한 회전(YAW축)이 가능하도록 추가된 턴테이블의 구동 사양이다.
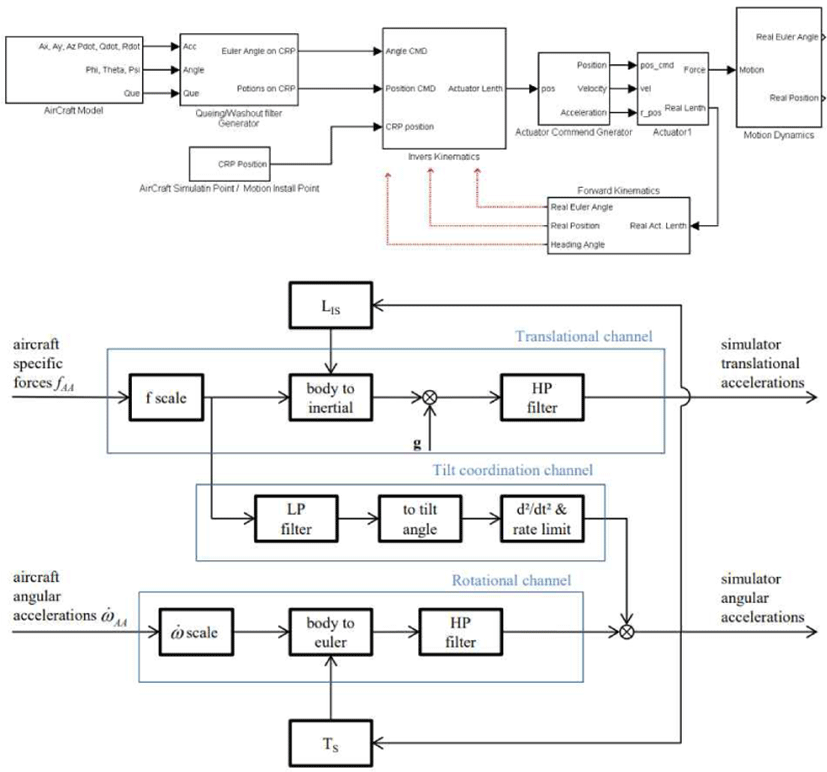
모션시스템은 제한적인 각도와 위치의 운용범위를 가진다. 따라서 일반적으로 적용대상 시뮬레이션 모델의 가속도 명령에 대하여 wash-out filter를 적용하여 일종의 체감효과를 적용하고, 중력에 의한 자세변화체감에 있어서는 적절한 작용함수나 튜닝요소, low-pass filter를 적용하여 구성(coordination angle)한다. 이러한 모션시스템 제어방식을 Classical Motion Control[1] (Fig. 3)이라 하며, 이 알고리즘을 기본 적용하였다.
이 필터링 기법은 Schmidt, S. F. and Conrad, B. 의 논문, “Motion drive signals for piloted flight simulators,”[2]에서 처음 공식화되었는데, 단일 축 시스템의 아이디어에서 시작하여 역기구학 접근으로 기구학적 완전 안정형태인 6도 자유도(6-DOF) 모션 플랫폼을 위한 첫 번째 시도였다. 이 알고리즘은 이후 3-DOF[3], [4] 및 6-DOF 플랫폼[5]을 포함하는 수많은 비행 및 자동차 시뮬레이터에서 구현되었다. 이후 제한적인 범위 내에서 비용함수를 적용한 최적화 기법을 적용한 시도들이 있었다.[5][6][7] 하지만 본 과제에서는 기존 기법들과는 달리 헬기나 차동차 시뮬레이터와 같은 비교적 빠른 움직임을 모의하는 가속도 추종 시뮬레이터에 비해 정적이며 느린 자세추종 시뮬레이터에 대한 기술이며, 2.2.2절에서 이러한 정적 자세모의 제한범위를 벗어난 항공기 자세가 다시 제한범위 이내로 회복될 때 움직임에 대한 이질감해소 방법을 제시 한다.
턴테이블의 회전지령은 항공기 헤딩값과 모션 초기값의 차를 이용하여 coordination channel 각도 및 속도명령으로 적용하였으며, 항공기 각가속도 ṙ에 대한 체감은 classical control에 따라 6축 모션의 상부 플렛폼에 high-pass wash-out filter를 적용하여 각각 분리 구성하였다. 그 결과, Fig. 4와 같이 항공기 헤딩각도 변화에 따라 상부 턴테이블이 회전하고, 회전 각도를 이용하여 모션시스템 제어기 구조를 변경하여야 한다.
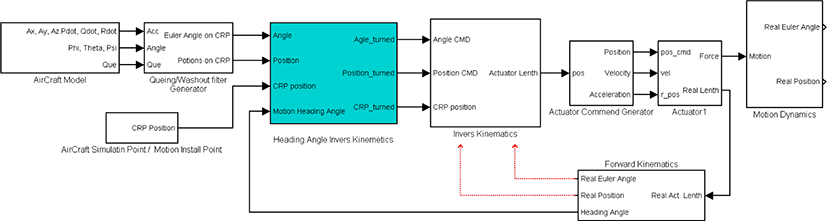
본 논문에 적용한 모션시스템은 턴테이블 위에 모션시스템을 적용하는 것과는 달리 모션시스템 상부 플레이트에 턴테이블을 적용하였다. 이 경우, 자세값을 비롯한 모든 명령값에 다음 식과 같은 회전변환을 적용하여야 한다. Classical motion control algorism에 상부 플렛폼에 적용한 턴테이블의 회전결과를 입력으로 각도명령(Angle_cmd)과 위치명령(Position_cmd), 그리고 CRP(Command Reference Position)의 위치를 회전변환하였다.
여기서,
ψmotion:모션시스템 헤딩 제어명령
ψaircraft0:모션항공기 시뮬레이션 헤딩명령
ψaircraft:모의항공기 헤딩값
ψadd:비행착각을 위한 추가요소
ϕcmd : 롤 각 제어 명령
θcmd : 피치각 제어명령
Δxcmd : surge 변화량 제어명령
Δycmd : sway 변화량 제어명령
이다.
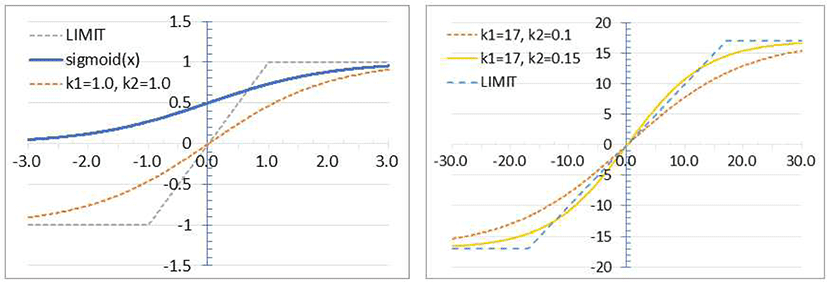
모션시스템은 근본적으로 제한된 각도 범위내에서 동작한다. Classical control의 low-pass filter가 적용된 coordination channel 항공기 자세각 모의부에 일반적으로 사용하는 제한함수[10]를 적용하면, 해당 각도 이상을 모의하는 시뮬레이션 상황에서 다시 제한범위 이내로 일정한 각속도로 진입하는 구간에서 미분 불가능한 자세추종 명령에 의한 순간적인 움직임을 보이게 되고, 이때 이질감이 동반된다. 이러한 이질감을 줄이기 위하여 본 저자는 Fig. 5와 같이 sigmoid function[11]을 활용한 제한함수 fsigmoidLIMIT(x)을 생성하고 적용하였다. 여기서 x에는 모션자세명령 롤/피치가 적용된다.
여기서, k1은 제한값이며, k2 는 입력에 관한 튜닝상수이다. 본 과제에서는 k1 = 17deg 로 제한하여 자세각을 모의하였으며, k2 = 0.1 를 적용하였다. 이는 모션 제한범위 ±23.8〬 내에서 Rotational-High-pass filter 큐잉요소에 적용될 모션자세 운용범위를 7.8〬 확보함을 의미한다. Fig. 6은 턴테이블 구동을 하지 않은 상태에서 fsigmoidLIMIT(x)를 적용한 시뮬레이션 결과로서 미분 가능한 형태로 제한영역에서 부드러운 모션제어 명령을 보임을 확인할 수 있다.
일반적으로 모션시스템은 역기구학으로 계산된 엑츄에이터에 대한 길이/속도 지령을 통해 구동되어진다. 이는 모션의 자세명령에 대한 Open-loop 제어로서 정상상태 수렴에 대한 성능만을 보장하며, 운동성능을 가시적으로 보이거나 평가를 위해서는 실시간 엑츄에이터의 길이를 이용한 순기구학의 계산이 필수적이다.
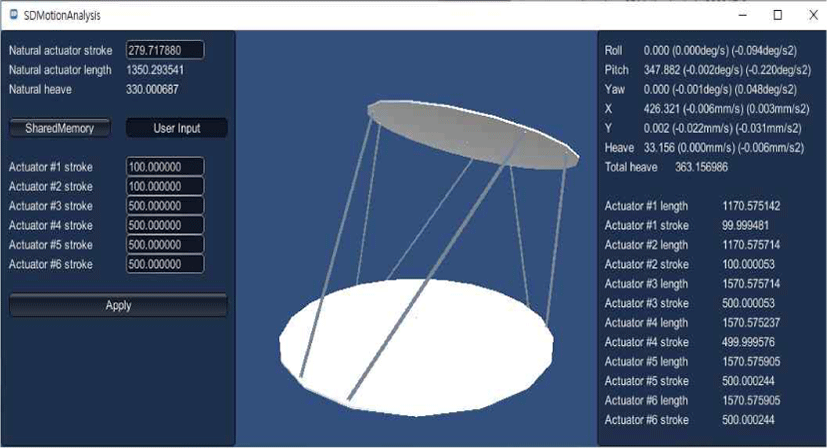
이러한 순기구학의 계산 방법에는 Newton-Raphson기법을 이용하거나[8], 신경망을 이용하는[9] 방법이 있었다. 하지만 이러한 계산방법은 이해가 어렵고 구현하기가 까다로운 단점이 있다. 따라서 개발 입장에서 직관적이면서도 시스템 개발의 활용도가 높은 게임엔진(여기서는 Fig. 7과 같은 Unity3D와 물리엔진)을 이용한 방법을 소개하고자 한다. 간단히 엑츄에이터 힌지 포인트와 상/하부 플레이트를 구성하고, 연결파라미터 구속조건을 Table 3과 같이 입력하고, 실시간 힌지 포인트의 거리 즉, 엑츄에이터 길이를 업데이트 하여 시뮬레이션 되는 상부플레이트의 각도와 위치값을 산출할 수 있다. 간단한 입력만으로 쉽게 구현할 수 있고, 이미지 랜더링을 포함하여 가시적인 효과를 부여할 수 있으므로 개발업체에서의 활용도와 소프트웨어 개발비용 절감을 기대할 수 있을 것으로 예상된다.
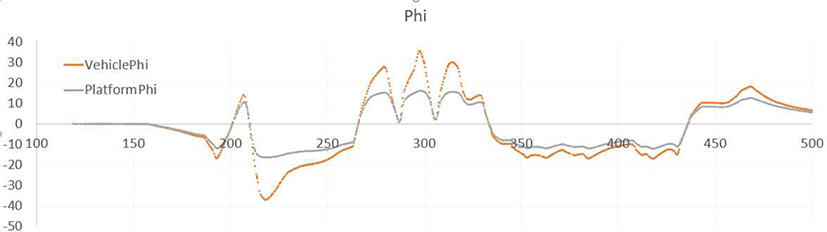
시뮬레이션 테스트 초기 조건으로 항공기(aircraft) Heading(Yaw)을 120도로 설정하였으며, 바닥에 고정된 모션시스템(motion)과는 120도의 Heading Offset을 가진 상태로 시뮬레이션이 진행되었다. Fig. 8은 이러한 제어 명령 시뮬레이션의 결과를 보여주며, 제일 위쪽의 Yaw 그래프를 보면 스튜어트 플렛폼에 360도 무한 회전을 하는 턴테이블을 적용함으로써 바닥에 고정된 모션시스템(motion)의 Yaw 값이 항공기(aircraft)의 Heading(Yaw) 값과 120도 Offset을 유지하면서 잘 추종하여 따라가는 것을 확인할 수 있다.
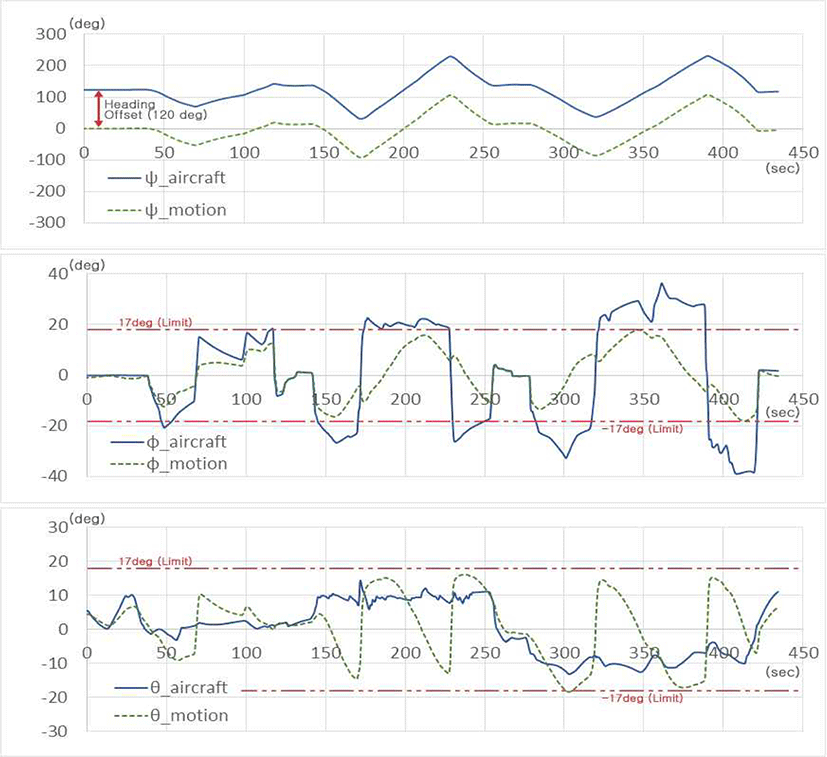
이륙후 좌우 선회비행을 실시하며, 자유 비행을 수행하였으며, 360도 자유로운 Yaw축 회전이 가능한 턴테이블로 인한 모션시스템(motion)의 헤딩각(Yaw)의 변화에 따라 회전변환된 모션시스템(motion)의 롤각, 피치각이 의도한 바와 같이 모션 턴테이블 헤딩각 90°(Fig 8 그래프의 약 170sec지점)에서 서로 반전되어 모의됨으로서 회전변환이 잘 적용됨을 확인할 수 있으며, Sigmoid Limit 함수 또한 반영되어 모션 상부 플렛폼의 자세각은 제한된 ±17deg 각도를 벗어나지 않고 부드럽게 모의됨을 확인할 수 있다.
Ⅲ. 결론 및 향후 연구
상부 플렛폼에 턴테이블을 적용한 모션시스템에 대한 명령발생기(command generator)를 구성하여 시뮬레이션하고, 모션시스템에 테스트 하였다. 향후는 조종석을 장착한 상태로 모션시스템의 체감적 요소를 튜닝하여 완성하고, 이후 헤딩각도에 대한 변화에 따라 재구성한 제어명령의 오차로 인한 정성적인 이질감이 최소화가 되도록 튜닝할 계획이다.
순기구학 해석을 위하여 유니티를 활용한 새로운 개념의 순기구학 해석을 적용함으로써 참고문헌에서의 순기구학 계산법을 적용하고, 검증하는 개발비용에 비해 저렴하고, 활용도가 높았다고 사료된다. 향후 이렇게 제시한 해석방법의 적용 시 발생하는 동적오차를 최소화하기 위한 방안에 대한 연구로서 테스트 포인트를 선정하고, 이를 신경망 및 수치해석기법에 의한 실시간 계산 결과와 비교할 필요성이 도출되었으며, 최종적으로 본 연구에서는 항공기 모델의 헤딩각 명령이 아닌 추가적인 헤딩각 명령(ψadd)을 구성하여 정량적인 공간정위상실적인 요소를 인가함에 따른 조종사의 반응과 회복에 관한 연구를 할 수 있는 테스트 절차와 방안을 수립하고자 한다.