지구-화성 행성 간 임무를 위한 전이 궤도 및 발사 윈도우 분석

김, 필은

doi:10.12985/ksaa.2025.33.2.019

J. Korean Soc. Aviat. Aeronaut. 2025; 33(2):19-27

pISSN: 1225-9705, eISSN: 2466-1791

DOI: https://doi.org/10.12985/ksaa.2025.33.2.019

Original Article

지구-화성 행성 간 임무를 위한 전이 궤도 및 발사 윈도우 분석

김필은 ^*

Transfer Orbits and Launch Window Analysis for Earth-to-Mars Interplanetary Missions

Pileun Kim ^*

Author Information & Copyright ▼

^*한국항공대학교 AI자율주행시스템공학과 조교수

연락저자 E-mail : pkim@kau.ac.kr 연락저자 주소 : 경기도 고양시 덕양구 항공대학로 76

© Copyright 2025 The Korean Society for Aviation and Aeronautics. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Apr 20, 2025; Revised: Apr 28, 2025; Accepted: May 14, 2025

Published Online: Jun 30, 2025

ABSTRACT

This paper presents an analysis of Earth-to-Mars transfer trajectories using classical astrodynamics approaches including Hohmann transfer, Lambert’s solution, and the patched conic approximation. The Earth-Mars trajectory is modeled in three phases: Earth departure via hyperbolic orbit, heliocentric transfer orbit, and Mars approach. The transfer orbit, which dominates the mission path, is designed using Lambert's problem, considering arbitrary departure and arrival dates. Key design parameters such as C3, the characteristic energy, are evaluated to assess mission feasibility. Case studies using NASA’s Curiosity (2011) and Perseverance (2020) missions show that the proposed method yields arrival date predictions within 1% of actual arrival times under the assumption of minimum C3 launch conditions. The fork-chop plot method is introduced to visualize and select optimal launch windows based on C3 and time of flight. Based on the synodic period between Earth and Mars, the paper suggests October 2026 as a feasible candidate for the next launch, with an estimated arrival in August 2027. The analysis supports the validity of the approach and provides a practical reference for future Mars transfer trajectory design.

Keywords: Interplanetary Transfer Orbit(행성 간 전이 궤도); Earth-Mars Trajectory(지구-화성 궤적); Characteristic Energy C3(특성 에너지); Fork-Chop Plot(포크-찹 플롯); Launch Window Analysis(발사 윈도우 분석)

Ⅰ. 서 론

우주는 광대하고 무한하며 만약 생명체가 지구에만 존재한다면, 이러한 규모는 비효율적일 수밖에 없다. 이에 따라 인류는 지구 외 생명체 존재 가능성을 탐색해 왔으며, 그 시작점 중 하나가 화성이다. 화성은 태양계에서 네 번째 궤도에 위치한 행성으로, 대기, 자전 주기, 지형, 계절 변화 등 여러 면에서 지구와 유사한 특징을 지닌다. 과거 액체 상태의 물이 존재했을 가능성, 비교적 얕은 중력장, 탐사에 용이한 환경 등으로 인해 생명체 존재 가능성과 거주 가능성 측면에서 가장 유력한 후보로 간주되어 왔다. 화성에 대한 탐사는 1965년 미국의 마리너 4호가 화성에 근접하여 표면 사진을 지구로 전송하면서 본격화되었다. 이후 수십 차례의 궤도선, 착륙선, 탐사로봇 미션이 진행되었으며, 현재까지도 탐사는 지속되고 있다. 최근에는 민간 우주 기업 SpaceX가 주도하는 화성 이주 계획이 현실적인 목표로 부상하고 있다. 일론 머스크는 인류의 다행성 거주를 목표로 삼고, 수백 명의 인류를 화성으로 이주시킬 수 있는 대형 발사체 ‘Starship’ 개발을 추진하고 있다. 이러한 흐름은 단순 탐사 차원을 넘어, 화성을 장기적인 거주지 및 이주 대상으로 간주하는 시대가 도래하고 있음을 시사한다.

화성 이주 혹은 장기 탐사를 위해서는 정밀한 행성 간 궤도 설계가 필수적이다. 일반적인 지구-화성 간 우주선 비행은 세 단계로 구성된다. 첫 번째는 지구 중력장을 이탈하는 쌍곡선 탈출 궤도, 두 번째는 태양 중심의 전이 타원 궤도, 세 번째는 화성 중력장으로 진입하는 쌍곡선 진입 궤도이다. 이 중 전이 궤도는 전체 항로의 99% 이상을 차지하며, 전체 임무에서 가장 중요한 구간이라 할 수 있다.

본 연구는 지구에서 화성까지의 전이 궤도 및 발사 윈도우를 결정하는 데 중점을 두고 있으며, 다양한 전이 궤도의 ΔV 요구량과 지구-화성 간 상대 위치를 기반으로 궤적 효율성을 비교한다. 여기서 ΔV는 궤도 변경 시 필요한 속도 변화량을 의미하며, 이는 우주선이 현재 궤도에서 목표 궤도로 전이하기 위해 추진력으로 제공해야 하는 에너지 요구량과 직결된다. 궤도 계산에는 구면 삼각법과 램버트 알고리즘을 활용하였으며, 행성의 궤도 정보는 JPL에서 제공하는 DE405 천체력(ephemeris)을 기반으로 한다. 본 논문의 결과는 향후 화성 탐사 및 이주 미션의 궤도 최적화에 기초 자료로 활용될 수 있다.

Ⅱ. 본 론

2.1 행성 간 전이 궤도의 이론적 배경

2.1.1 Hohmann Transfer

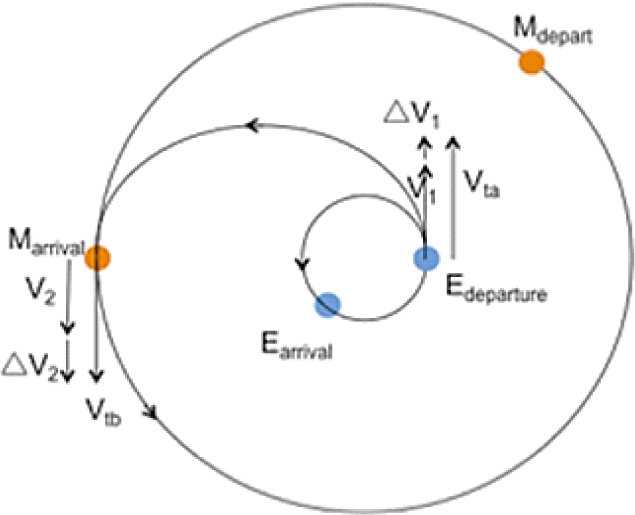
행성 간 임무를 계획할 때 가장 기본적으로 고려되는 요소 중 하나는 호만 전이 궤도이며, Fig. 1에 나타나 있다. 이는 해석이 가장 간단하고 에너지 효율이 가장 높은 전이 방법으로 알려져 있다. 단, 이 궤도를 적용하기 위해서는 전이 대상 행성들이 동일한 궤도면 상에 있어야 하며, 적절한 위치에 배치되어 있어야 한다. 이러한 기회는 일정 주기로 발생하며, 그 주기는 호만 전이 조건으로부터 유도할 수 있다.

Fig. 1. Hohmann transfer trajectory

Download Original Figure

호만 전이는 타원 궤도를 따라 출발 행성의 공전 궤도에서 도착 행성의 공전 궤도로 우주선을 이동시키는 방식이다.

출발점인 지구에서의 태양 중심 원형 공전 속도는 식 (1)과 같고,

v c 1 = G M r 1

(1)

전이 궤도의 장반경(semi-major axis)을

a t = r 1 + r 2 2

(2)

이라 할 때, 근일점에서의 전이 궤도 속도는

v t 1 = G M (2 r 1 − 1 a t)

(3)

가 된다. 이에 따라 출발 시 소요되는 1차 ΔV는

Δ v 1 = v t 1 − v c 1

(4)

로 계산된다.

우주선은 해당 전이 궤도를 따라 이동하며, 원일점에 도달했을 때 도착 행성인 화성 궤도로의 진입을 위해 2차 ΔV를 수행한다. 이때 화성의 원형 공전 속도는

v c 2 = G M r 2

(5)

이며, 전이 궤도 상 원일점에서의 속도는

v t 2 = G M (2 r 2 − 1 a t)

(6)

이므로, 화성 진입 시 필요한 ΔV는 식 (7)과 같고

Δ v 2 = v c 2 − v t 2

(7)

그러므로 총 ΔV는 식 (8)과 같다.

Δ v t o t = Δ v t + Δ v 2

(8)

이 분석은 지구와 화성의 궤도가 원형이며 같은 평면상에 존재한다는 이상적인 가정하에 이루어진다. 그러나 실제로는 행성의 궤도는 원형도 아니고 동일 평면상에 있지도 않기 때문에 호만 전이를 그대로 적용하기에는 한계가 존재한다.

2.1.2 Lambert Problem

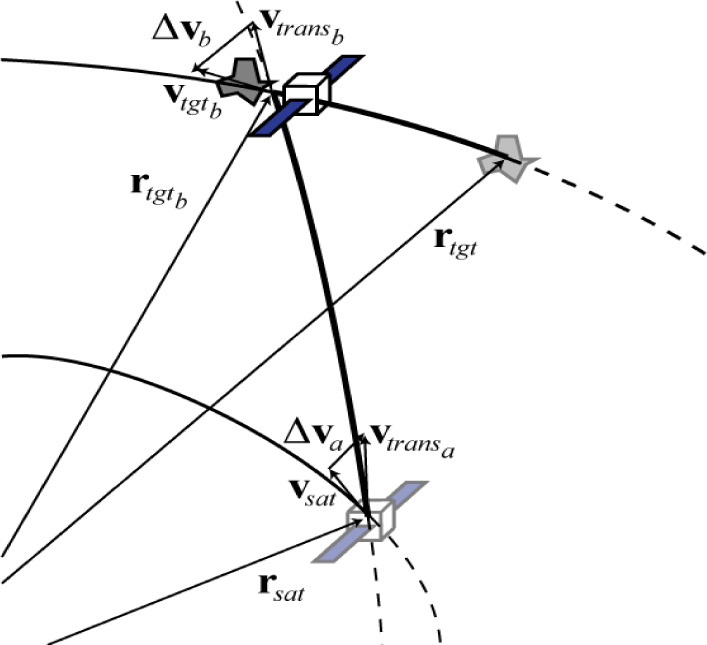
행성 간 임무 설계에서 핵심적인 문제 중 하나는 특정 시점에서 출발하여 다른 시점에 도착하는 궤적을 설계하는 것이다. 이때 출발 시점과 도착 시점은 임의로 설정할 수 있지만, 이에 따라 요구되는 추진 에너지가 크게 달라진다. 램버트 문제는 Fig. 2와 같이 주어진 출발점과 도착점의 두 위치 벡터와 비행시간 Δt를 기반으로 이를 연결하는 전이 궤도를 결정하는 방법이다. 이 문제를 해결함으로써 전이 궤도의 궤도 요소를 정의할 수 있으며, 이를 통해 출발 및 도착 시의 속도 벡터를 구할 수 있다.

Fig. 2. Lambert targeting problem

Download Original Figure

램버트 정리에 따르면, 출발점에서 도착점까지의 비행시간은 궤도의 이심률과 무관하며, 두 위치 벡터의 크기 합, 장반경, 두 점을 잇는 코드 길이에만 의존한다. 램버트 문제의 해법은 다양하게 제시되어 있으며, 본 연구에서는 범용 변수 공식을 기반으로 문제를 해결하였다.

2.1.3 Patched Conic Method

패치드 코닉 기법은 3체 문제의 복잡성을 회피하기 위해 각 구간을 단순한 2체 문제로 근사하는 방법이다. 구체적으로, 각 천체의 중력 영역 (sphere of influence, SOI)을 기준으로 궤도를 분할하고, 해당 영역 내에서는 중심력장 하의 쌍곡선 또는 타원 궤도로 근사하여 계산한다. 예를 들어, 우주선은 출발 행성인 지구의 중력장 내부에서 행성 중심 궤도를 따라 이탈하고, SOI를 벗어난 시점부터는 태양 중심의 궤도를 따라 이동한다. 이는 첫 번째 ‘패치’이다. 도착 행성인 화성의 SOI에 진입한 이후에는 다시 행성 중심 궤도로 전환되며, 이것이 두 번째 패치이다. 이 방식은 단순한 2체 역학만으로 행성 간 이동에 필요한 속도 변화량(ΔV)을 근사할 수 있게 해주며, 초기 임무 계획 및 타당성 분석에서 매우 유용하다. 또한 여러 전이 궤도 및 캡처 전략을 비교 평가할 수 있는 기준값으로도 사용된다.

2.2 전이 궤도 임무 설계

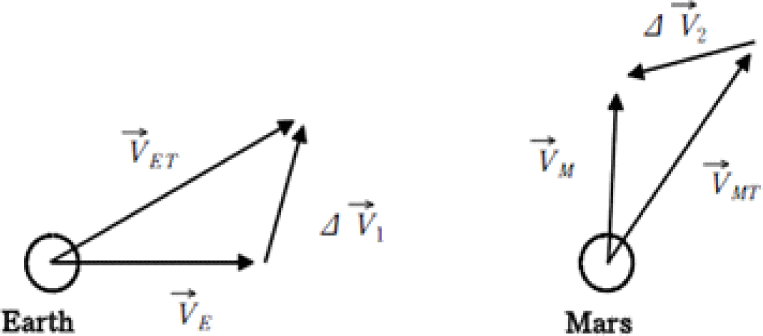
지구 궤도에서 전이 궤도로, 그리고 전이 궤도에서 화성 궤도로의 진입에 필요한 속도는 식(9)와 Fig. 3을 통해 정의된다.

Fig. 3. Required velocity vectors

Download Original Figure

Δ V 1 = V E T − V E Δ V 2 = V M − V M T

(9)

여기서 각 변수의 의미는 다음과 같다.

V_ET : 지구 위치에서 전이 궤도의 속도 벡터

V_MT : 화성 위치에서 전이 궤도의 속도 벡터

V_E : 태양 기준의 지구 속도 벡터

V_M : 태양 기준의 화성 속도 벡터

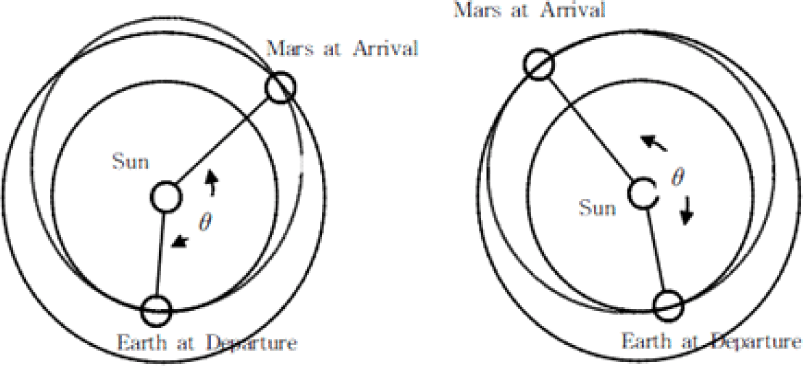
전이 궤도의 유형은 두 가지로 나뉜다. Type I은 출발 시점에서 지구와 도착 시점에서 화성 사이의 위상각이 180도 미만인 경우이며, Type II는 그 위상각이 180도 초과인 경우이다. 위상각은 출발일 기준 지구의 위치와 도착일 기준 화성의 위치 사이의 각도로 정의된다. 이는 Fig. 4에 잘 나타나 있다. Type I 궤도는 비행시간이 짧다는 장점이 있으며, Type II 궤도는 출발 날짜 측면에서 유리하다.

Fig. 4. Type of transfer orbit

Download Original Figure

행성 간 임무를 수행할 수 있는 적절한 행성 배열 주기를 회합 주기(synodic period)라 하는데 즉 두 천체의 상대적 위치가 다시 같아지는 주기를 말하며, 식 (10)과 같이 표현된다.

1 S = | 1 T E − 1 T M |

(10)

여기서 T_E와 T_M은 각각 지구와 화성의 공전 주기, S는 회합 주기이며 지구와 화성의 회합 주기는 약 2,135년이다.

지구에서 화성으로의 행성 간 전이는 실제로는 태양, 지구, 화성, 우주선을 포함한 4체 문제에 해당된다. 그러나 patched conic method를 활용하면 각 구간을 2체 문제로 근사할 수 있다. 따라서 궤도는 세 단계로 나뉜다: 1) 지구 출발 단계: 궤도는 쌍곡선이며 태양과 화성의 영향은 무시하고 지구와 우주선만 고려한다. 2) 태양 중심 전이 단계: 궤도는 타원이며 지구와 화성의 영향은 무시하고 태양과 우주선만 고려한다. 3) 화성 도착 단계: 궤도는 쌍곡선이며 태양과 지구의 영향은 무시하고 화성와 우주선만 고려한다.

이에 따라 지구와 화성 간 궤도 설계 절차는 다음과 같다.

지구에서 출발일과 화성 도착일을 결정함으로써 전체 임무 기간의 설정
천체력을 이용하여 해당 날짜의 위치 및 속도 계산
지구-화성 간 태양 중심 전이 궤도 설계
전이 시간과 임무 시간을 일치시키는 궤도 요소 결정
지구 출발 쌍곡선 궤도 설계
화성 진입 쌍곡선 궤도 설계

이 중 가장 핵심은 태양 중심의 전이 궤도 설계이며, 이로부터 필요한 ΔV 및 태양 기준 우주선의 상대 속도를 계산할 수 있다.

2.3 천체력을 이용한 궤도 계산

지구-화성 간 전이 궤도는 태양 중심의 타원 궤도이며, 출발일 기준 지구의 위치와 도착일 기준 화성의 위치를 정확히 지나야 한다. 따라서 전이 시간은 전체 임무 시간과 일치해야 하며, 이는 타원 궤도의 출발점에서 도착점까지의 진근점 이각(true anomaly)을 반복 계산하여 궤도를 수치적으로 구해야 한다.

태양계 내의 행성 궤도는 시간에 따라 궤도 요소(장반경, 이심률, 경사 등)가 미세하게 변하며, 이는 타 행성의 섭동 효과에 기인한다. 이 섭동 효과는 정확한 행성 위치 계산에 있어 매우 중요한 요소이다. 따라서 정확한 천체력을 계산하는 것이 중요한데 이를 계산하는 방법은 두 가지가 있다: 1) J2000 기준 좌표계를 이용하는 방식, 2) 평균 춘분점을 기준으로 한 방식.

본 연구에서는 JPL Solar System Dynamics에서 제공하는 “Keplerian Elements for Approximate Positions of the Major Planets”을 참고하였다. 이 자료는 1800년부터 2050년까지의 기간에 대해 J2000 기준 평균 황도와 춘분점을 기준으로 한 궤도 요소 및 그 변화율을 제공한다.

각 행성의 태양 중심 궤도를 2000/01/01을 기준으로 한 천체력으로 나타낼 수 있다.

O r i b t E l e m e n t = a 0 + a 1 T + a 2 T 2 + a 3 T 3

(10)

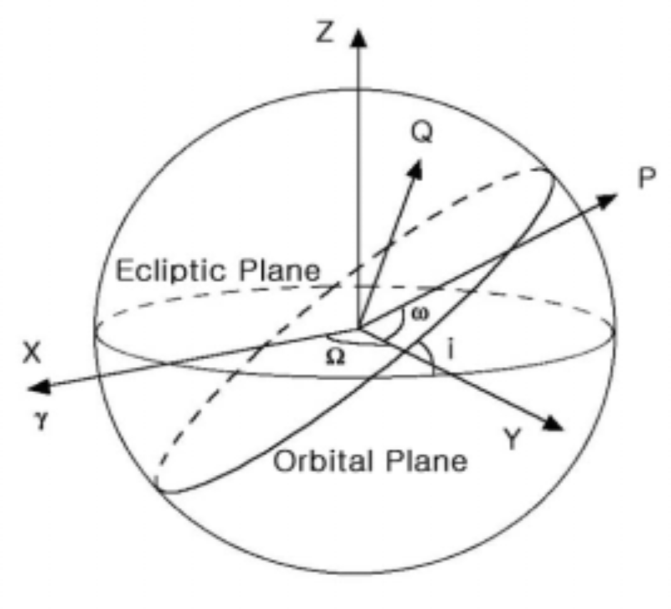
식(10)에 대한 계수는 Table 1과 Table 2에 각각 지구와 화성에 해당하는 값들이 제시되어 있다. 여기서 a는 장반경, e는 이심률, i는 궤도 경사각, Ω는 승교점 경도, ω는 근일점 경도, L은 태양 중심을 기준으로 한 평균 경도이며 Fig. 5에 나타나 있다.

Table 1. Coefficients of Earth orbit elements

	a ₀	a ₁	a ₂	a ₃
L	100.466449	+36000.7698231	+0.00030368	+0.000000021
a	1.000001018
e	0.01670862	-0.000042037	-0.0000001236	+0.00000000004
i	0
Ω	0
ω	102.937348	+1.7195269	+0.00045962	+0.000000499

Download Excel Table

Table 2. Coefficients of Mars orbit elements

	a ₀	a ₁	a ₂	a ₃
L	355.433275	+19141.6964746	+0.00031097	+0.000000015
a	1.523679342
e	0.09340062	+0.000090483	-0.0000000806	-0.00000000035
i	1.849726	-0.0006010	+0.00001276	-0.000000006
Ω	49.558093	+0.7720923	+0.00001605	+0.000002325
ω	336.060234	+1.8410331	+0.00013515	+0.000000318

Download Excel Table

Fig. 5. Coefficients of orbit elements

Download Original Figure

또한, T는 기준 시점로부터 세기 단위의 경과한 시간이다. 기준 시점은 2000년 1월 1일이며, 이후 경과 시간 T는 식 (11)과 같이 계산된다.

T = J u l i a n D a y − 2451545 36525

(11)

여기서 2451545는 2000년 1월 1일의 줄리안 데이 에 해당한다.

이 궤도 요소들을 통해 각 행성의 위치와 속도를 구한 후, Fig. 5의 궤도 좌표계(P, Q, W)에서 태양 중심 좌표계(X, Y, Z)로 변환함으로써 실제 궤적 해석이 가능하며 식 (12)와 식 (13)에서 그 변환식을 제공하고 있다. 여기서 춘분 방향은 황도면에서 X축이고, X축에 수직인 방향은 적도면에서 Y축이며, Z 방향은 X×Y이다. P와 Q는 궤도면에서 서로 수직이며, 여기서 P는 근일점 방향을 나타내고 W 방향은 P×Q이다.

[X Y Z] = A 3 (Ω) A 1 (i) A 3 (ω) [P Q W] A 3 (Ω) = [cos Ω − sin Ω 0 sin Ω cos Ω 0 001] A 1 (i) = [100 0 cos i − sin i 0 sin i cos i] A 3 (ω) = [cos ω − sin ω 0 sin ω cos ω 0 001]

(12)

[X Y Z] = [c ω c Ω − s ω c i s Ω − s ω c Ω − c ω c i s Ω s i s Ω c ω s Ω + s ω c i c Ω − s ω s Ω + c ω c i c Ω − s i c Ω s ω s i c ω s i c i] [P Q W] = [P x Q x W x P y Q y W y P z Q z W z] [P Q W]

(13)

식 (13)을 시간 미분하면 식 (14)와 같다.

[X ˙ Y ˙ Z ˙] = [P x Q x W x P y Q y W y P z Q z W z] [P ˙ Q ˙ W ˙]

(14)

또한, 궤도 좌표계의 위치 벡터 성분과 그에 대한 시간 도함수는 식 (15)와 같으며 태양 중심 좌표계의 위치 벡터 성분과 그에 대한 시간 도함수는 식 (16)과 같다.

[P Q W] = [a (cos E − e) b sin E 0] [P ˙ Q ˙ W ˙] = [− G M ⊙ a a r sin E G M ⊙ a b r cos E 0]

(15)

r → = a P → (cos E − e) + b Q → sin E v → = G M ⊙ a 1 r (b Q → cos E − a P → sin E)

(16)

여기서 a와 b는 궤도 프레임의 장반경, 단반경이며, P ⃗와 Q ⃗는 궤도 프레임의 위치 벡터이다. 편심 이상(eccentric anomaly, E)은 뉴턴-랩슨 수치해석법을 사용하여 케플러 방정식으로 계산한다.

2.4 이탈 속도 조건: C3의 중요성

행성 간 임무 설계에서 가장 중요한 요소 중 하나는 C3 값이다. 여기서 C3는 지구 중력권을 이탈하여 태양 중심 전이 궤도로 진입할 때 필요한 속도의 제곱을 의미한다. 이 값은 우주선의 성능, 즉 탑재 가능한 연료량 및 추진계 설계와 밀접한 관련이 있기 때문에 행성 간 임무를 위한 전이 궤도를 설계할 때 반드시 고려되어야 한다. C3는 각 벡터 성분으로 식 (17)과 같이 계산할 수 있다.

V E = (X 1, Y 1, Z 1) V E T = (X 2, Y 2, Z 2)

(17)

여기서 V_E 는 지구를 이탈하는 시점에서 우주선의 태양에 대한 상대 속도이고, V_ET는 전이 궤도 진입에 필요한 속도이다. 따라서 C3는 식 (18)과 같이 계산한다.

C 3 = (X 2 − X 1) 2 + (Y 2 − Y 1) 2 + (Z 2 − Z 1) 2

(18)

2.5 실제 사례 연구 및 적용 확장

화성 탐사 프로그램으로 유명한 'Curiosity'와 가장 최근에 발사된 'Perseverance'의 사례를 통해 본 논문에서 사용한 방법을 검증해 보고 확장 적용해 볼 것이다. 'Curiosity'는 2011년 11월 26일에 발사되어 화성에 도착일은 2012년 8월 6일이었다. 또한, 'Perseverance'는 2020년 7월 30일에 발사되어 2021년 2월 18일에 도착했다.

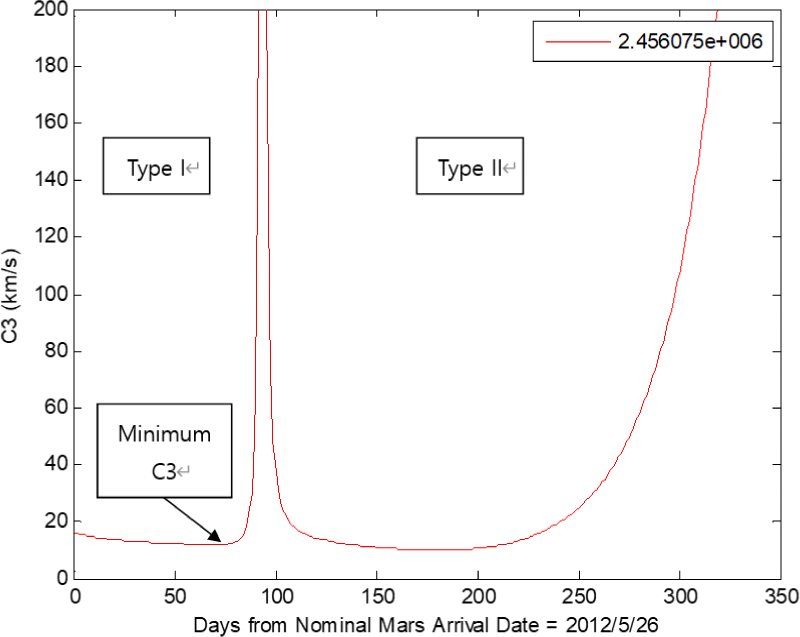
화성 도착일은 발사 6개월 후를 예상 도착일이 설정하고 최소 C3로 발사된다는 가정하에 도착일을 확인해 볼 수 있다. 먼저 'Curiosity'의 경우, 2012년 5월 26일을 예상 도착일로 설정하여 최소 C3값으로 실제 도착일을 찾을 수 있다. Fig. 6을 보면 최소 C3가 약 70일 후임을 확인할 수 있는데 2012년 5월 26일에서 70일 후면 2012년 8월 5일 경이며, 이는 실제 도착일과 하루 정도 차이임을 알 수 있다(Fig. 7).

Fig. 6. Minimum C3 plot for Curiosity

Download Original Figure

Fig. 7. Minimum C3 plot for Perseverance

Download Original Figure

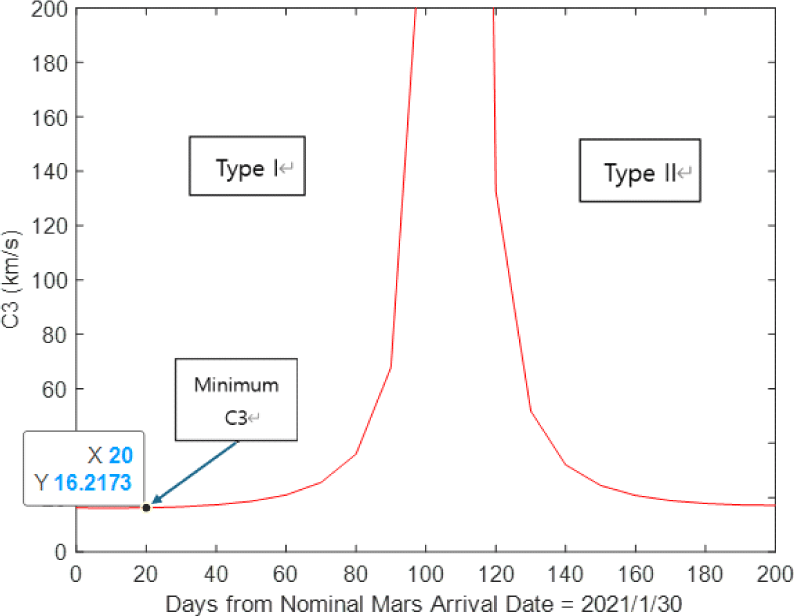
'Perseverance'의 경우, 2021년 1월 30일을 예상 도착일로 설정했고 최소 C3가 약 20일 후인데 이는 2021년 2월 19일임을 확인할 수 있다. 역시 실제 도착일과 하루 정도 차이임을 알 수 있으며, 따라서 본 논문에서 사용한 방법은 신뢰할 수 있다고 볼 수 있다. Table 3에 'Curiosity'와 'Perseverance' 탐사선의 지구-화성 전이 궤도의 케플러 요소값과 C3, v_∞가 제시되어 있다.

Table 3. Keplerian elements of transfer orbit

	Curiosity (Departure Nov 26, 2011 and Arrival Aug 6, 2012)	Perseverance (Departure July 30, 2020 and Arrival Feb 18, 2021)
L	189089650.4 km	199127740.4 km
a	0.2235	0.2377
e	0.34^o	2.2337^o
i	243.58^o	307.5709^o
Ω	165.8^o	356.3837^o
ω	168.14^o	207.193^o
C3	11.6848 km²/s²	14.3978 km²/s²
v _∞	3.3295 km/s	2.6897 km/s

Download Excel Table

지구와 화성의 회합 주기는 약 2.135년, 약 780일이다. 따라서 'Curiosity' 이후 화성에 탐사선을 보낼 수 있는 기회는 2014년 1월, 2016년 3월, 2018년 4월 이렇게 3번이 있었고 그 다음 윈도우 때 'Perseverance'가 2020년 7월에 발사된 것이다. 그렇다면 'Perseverance' 다음 기회는 2022년 7월과 2024년 9월, 2026년 11월에 또 다른 기회가 열려 있는 것이다. 따라서 본 논문에서 고려하는 발사 후보일은 2026년 11월 13일경으로 상정해 보았다. 그러면 6개월 후인 2027년 5월 13일로 예상 도착일이 설정할 수 있다.

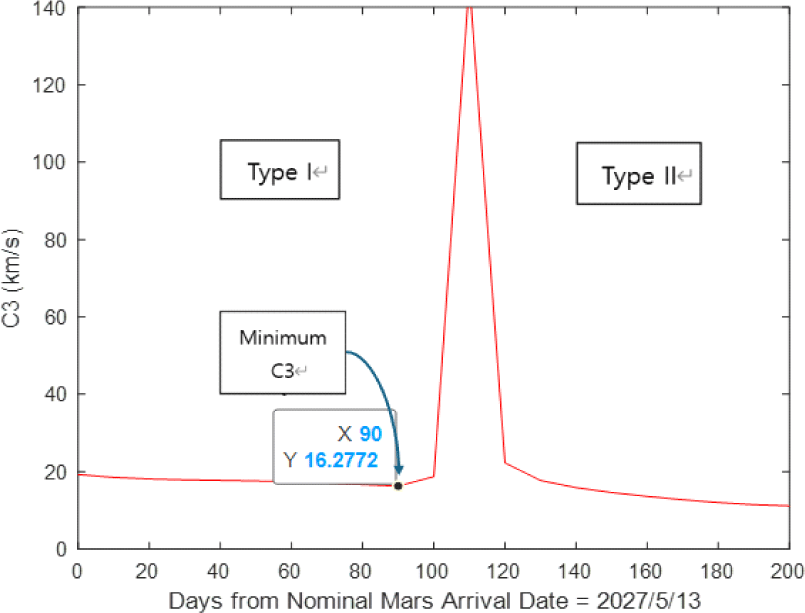
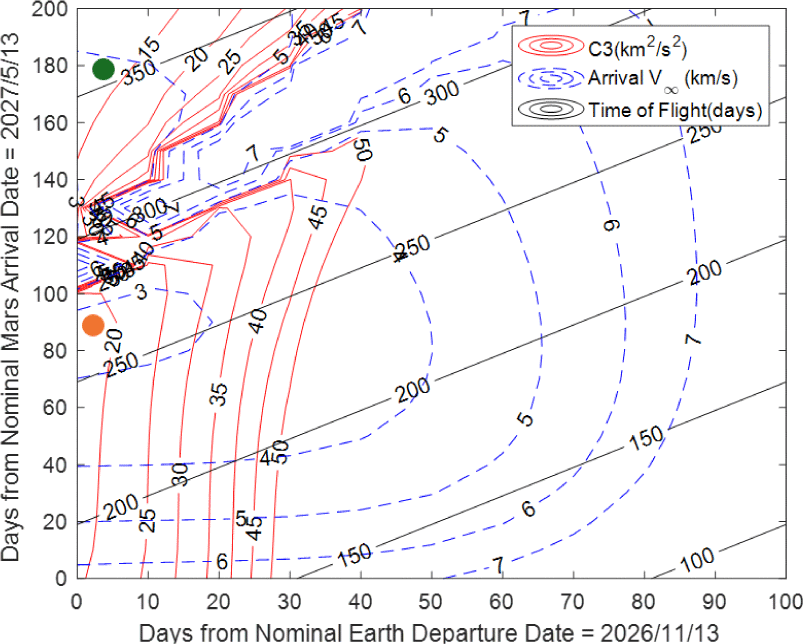
Fig. 8은 새로운 화성 탐사선의 C3 plot으로 최소 C3로 발사한다면 도착 예정일로 설정한 2027년 5월 13일보다 90일 후에 도착함을 알 수 있다. 따라서 새로운 화성 탐사선의 화성 도착일은 2027년 8월 10일이다.

Fig. 8. Minimum C3 plot for new launcher

Download Original Figure

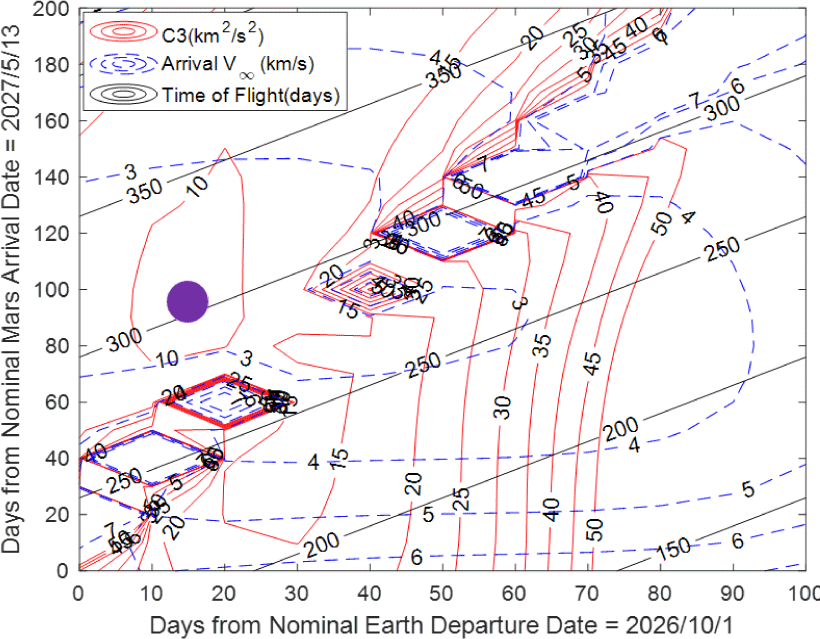
Fig. 9는 C3와 v_∞, 전이 시간을 나타내는 fork chop plot이다. 이 차트를 통해 원하는 C3와 v_∞, 전이 시간을 고려하여 적절한 출발일과 도착일을 결정할 수 있다. 주황색과 초록색 원이 plot의 왼쪽에 치우쳐 있는데, 이들은 서로 다른 전이 시간을 가지는 최소 C3와 v_∞를 나타낸다. 주황색 원은 Type-I으로 전이 시간이 약 270일이며, 초록색 원은 Type-II로 전이 시간이 약 350일이다. 이는 2026년 11월 13일을 출발일로 잡았을 때의 경우이다. 그러나 Fig. 9에서 볼 수 있다시피 plot 왼쪽부분을 더 관찰할 수 있다면 더 좋은 C3나 v_∞로 전이할 수 있을 수 있기 때문에 출발일을 2026년 10월 1일로 앞당겨서 다시 fork chop plot를 그려보면 Fig. 10과 같다.

Fig. 9. Fork chop plot (departure at 2026/11/13)

Download Original Figure

Fig. 10. Fork chop plot (departure at 2026/10/1)

Download Original Figure

여기서 보라색 원의 위치를 보면 10km²/s² 정도의 C3로 출발하여 3km/s보다 작은 v_∞로 화성에 도착하게 된다. 이는 Fig. 9에서 주황색과 초록색 원의 위치의 C3와 v_∞보다 더 좋은 조건으로 전이하게 되는 것으로 Fig. 9의 주황색 원 위치보다 비행 시간은 늘어나지만 효율적 측면에서 더 좋은 발사 시점으로 평가할 수 있다. 따라서 다음 화성에 보내기 좋은 시점은 2026년 10월 15일에 탐사선을 발사하는 것이며 약 300일의 비행을 거쳐 화성에 2027년 8월 10일에 도착하게 된다.

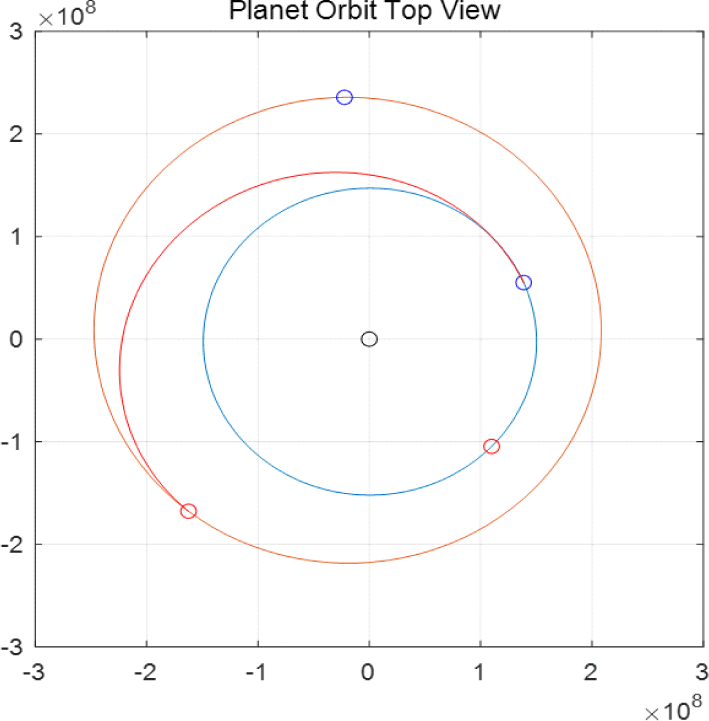
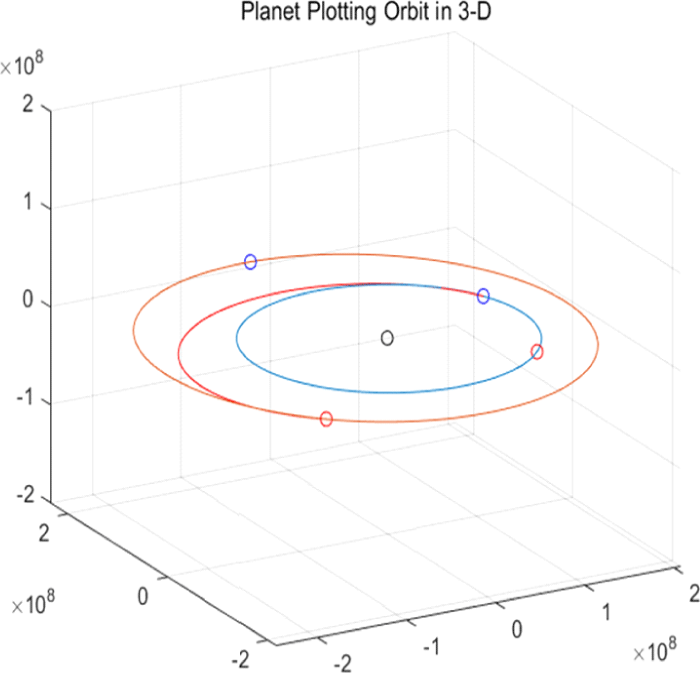
Fig. 11은 이와 같이 결정된 새로운 화성 탐사선이 지구에서 화성까지의 평면 상에서의 궤적을 보여주며, Fig. 12는 3차원 상에서의 궤적을 보여준다. 가운데 검은 색 원은 태양이며 하늘색 궤도가 지구 공전 궤도, 주확색 궤도가 화성 공전 궤도이다. 그리고 각 궤도에서 파란색 원이 발사 시점에서의 각 행성의 위치이며, 각 궤도에서 빨간색 원이 도착 시점에서의 각 행성의 위치이다. 또한, 지구 공전 궤도와 화성 공전 궤도 사이의 빨간색으로 표시된 지구-화성 간의 전이 궤도이다. Table 4에 새로운 화성 탐사선의 지구-화성 전이 궤도의 케플러 요소값과 C3, v_∞가 제시되어 있다. fork chop plot에서도 확인했지만 매우 적고 효율적인 C3와 v_∞로 지구에서 화성까지 전이함을 알 수 있다.

Fig. 11. Planet orbit top view

Download Original Figure

Fig. 12. Planet orbit 3D view

Download Original Figure

Table 4. Keplerian elements of transfer orbit

	New Mars explorer (Departure Oct 15, 2026 and Arrival Aug 10, 2027)
L	191328806.8 km
a	0.225
e	0.2837^o
i	201.68^o
Ω	194.7478^o
ω	197.81^o
C3	10.4297 km²/s²
v _∞	2.7932 km/s

Download Excel Table

Ⅲ. 결 론

지구-화성 궤도는 패치드 코닉 기법을 통해 지구 출발 쌍곡선 궤도, 태양 중심 전이 궤도, 화성 접근 쌍곡선 궤도의 세 단계로 분할하여 모델링할 수 있다. 이 중 전이 궤도는 전체 임무의 핵심 구간으로, 출발일과 도착일에 해당하는 행성의 위치 벡터를 기반으로 램버트 문제를 해결함으로써 설계할 수 있다. 그러나 지구와 화성은 동일한 궤도면에 있지 않기 때문에, 위상각이 180도에 가까워질수록 전이 궤도의 경사가 증가하고, 이에 따라 요구되는 C3 값이 급격히 증가하는 경향이 있다. 이는 임무 설계에 있어 큰 부담이 되며, 궤도 선택에 영향을 준다. 전이 궤도 설계 시, 임의의 출발일과 도착일을 바탕으로 C3를 계산하고, fork chop plot을 활용하여 원하는 추진량(ΔV)에 맞는 발사 윈도우를 결정할 수 있다. 본 논문에서는 'Curiosity'와 'Perseverance' 미션의 실제 사례와의 비교를 통해 제안한 방법의 유효성을 검증하였으며, 2026년 10월 발사를 상정한 궤도 설계 시나리오도 제시하였다. 향후 연구에서는 행성 중력권 내 쌍곡선 궤도의 정밀 해석, 화성 대기 진입 및 착륙 시 궤도 변환 방식, 실제 임무 적용을 위한 연료량 기반 최적화 분석 등에 대한 추가 심화 연구가 진행될 예정이다.

Acknowledgement

이 출판물은 2021년도 한국항공대학교 교비지원 연구비에 의하여 지원된 연구의 결과입니다.

References

Vallado, David A. "Fundamentals of Astrodynamics and Applications - Third Edition", Microcosm Press. Hawthorne, CA. 2007.

Kemble, Stephen. "Interplanetary Mission Analysis and Design", Springer. Chichester, UK. 2006.

Curtis, Howard D. "Orbital Mechanics for Engineering Students", Elsevier Butterworth-Heinemann. Burlington, MA. 2005.

Izzo. D., Hennes. D. and Riccardi. A., "Constraint handling and multi-objective methods for the evolution of interplanetary trajectories, " Journal of Guidance, Control, and Dynamics, 38(4), 2015, pp.792-800.

Yam. C. H., Di Lorenzo D. and Izzo. D., "Constrained global optimization of lowthrust interplanetary trajectories", IEEE Congress on Evolutionary Computation (CEC), IEEE Publ., Piscataway, NJ, 2010, pp. 1-7.

NASA JPL. "Solar System Dynamics Ephemerides", 2020, Available from: https://ssd.jpl.nasa.gov/ephem.html

So, E. J, Kim, K., and Kim, L., "A study on R&D critical factors affecting R&D Performance in aviation and aerospace industries", Journal of the Korean Society for Aviation and Aeronautics, 27(2), 2019, pp.26-36.

Lim, C. H, and Kim, J., "An effect of a corporation's network position in the Korean space industry on performance", Journal of the Korean Society for Aviation and Aeronautics, 29(4), 2021, pp.67-77.