Ⅰ. Introduction
Despite of technological advancements in the aviation industry, aircraft accidents caused by human errors among flight crew members continue to persist (Helmreich, 1997). To prevent accidents resulting from such human errors, it is not merely sufficient to enforce regulations; rather, the perception of safety behavior, where pilots actively participate in flight safety and adhere to regulations, must be established for it to be effective (Neal and Griffin, 2004).
Furthermore, safety behaviors not only impact aviation accidents but also influence attitudes and values related to worker safety in other industries such as railways, gas and nuclear facilities, and genetic accidents (Cooper, 2000).
Helmreich et al. (1998) emphasized that safety behaviors are influenced not only by individual traits but also by the organization to which the individual belongs (Helmreich, 1999).
O’Connor et al. (2011) highlighted that, while the technical aspects of flying are crucial in safety behavior, pilot safety behaviors require socio-psychological abilities such as communication, situation awareness, and workload management.
Previous research on safety behavior typically involved conducting surveys first, followed by evaluating the reliability of the questionnaire and categorizing and analyzing the questionnaire items.
However, subjective question formulated as a single sentence may be more efficient in investigating factors influencing safety behavior than using multiple questionnaire items.
For example, when examining the communication of flight crew members, six questionnaire items could be used, but it is also possible to pose a single question such as “Do you think the communication in the airline you work for is smooth?“
In this case, if respondents are clearly aware of the of the concept of “communication” in the survey, it can be replaced with a single question, and responses to subjective questions may vary based on flight hours and working environment. In such cases, considering the most rational value along with scores that may vary based on flight hours or environmental factors could be reasonable. Therefore, it is necessary to pose questions about safety behavior or variables explaining it in a single sentence and represent survey responses as uncertain data.
In this study, to analyze pilots’ perception of safety behavior, a combination of the traditional 5-point scale survey and subjective responses was employed. The subjective responses of flight crews, who are a group of experts with excellent intellectual abilities, were transformed into fuzzy numbers and analyzed.
The explanatory variables for pilot safety behavior were divided into detailed factors of Management Commitment to Safety (SM), Perceived Organizational Support (S), Staff and Equipment (SE), Colleague Commitment to Safety (CC), Collaboration & Involvement (CI), Flight Quality Assurance (QA), and Just Culture & Reporting (JC). The operational definition of these variables is as follows.
Firstly, Management Commitment to Safetyencompasses the trust in the safety performance of managers perceived by flight crew members. It involves the concept of managers resolving safety-related issues raised by flight crew members and showing support for the issues raised (Hansez at el., 2010).
Secondly, Perceived Organizational Support includes the extent to which organizational members perceive the organization recognizing and valuing the contributions and efforts of flight crew members towards flight safety, displaying a positive and supportive attitude (Krishnan et al., 2012).
Thirdly, Staff and Equipment signifies the company providing an adequate supply of proficient pilots and state-of-the-art safety equipment for flight safety (Riwo-Abudho et al., 2013).
Fourthly, Colleague Commitment to Safety pertains to the commitment of fellow pilots within the cockpit to safety performance (Burt el at., 2008).
Fifthly, Collaboration & Involvement is a concept that incorporates the degree of active collaboration and participation among pilots (Morrow et al., 1994).
Sixthly, Flight Quality Assurance denotes the overall activities employed by the airline for flight safety quality management (Xueyan et al., 2012).
Lastly, Just Culture & Reporting represents the concept of receiving appropriate feedback regarding events reported for flight safety, and the fair treatment of personal information protection and non-punitive systems for reporters (Liao et al., 2015).
The purpose of this study is to present a statistical model for the safety behavior of flight crew members through the analysis of safety behavior using fuzzy sets in conjunction with the traditional 5-point scale survey method. In Chapter 2, we identify the variables influencing safety behavior through structural equation modeling (SEM) and path analysis.
Then, in Chapter 3, we estimate a statistical model for safety behavior transformed into fuzzy numbers based on subjective responses. Using the estimated fuzzy regression model, we examine the differences in safety behavior based on flight hours and the airline of employment.
Ⅱ. Main Body
In this study, correlation analysis, t-test, ANOVA, structural equation modeling were conducted using survey constructed with a 5-point Likert scale. The survey aimed to investigate the perception of flight crew members regarding safety behavior and variables directly influencing safety behavior.
Through theoretical background and prior studies, the variables explaining the perception of safety behavior (Sb) among flight crew members were determined as Collaboration & Involvement (Ci), Staff and Equipment (Se), Perceived Organizational Support (S), Flight Quality Assurance (Qa), Management Commitment to Safety (Sm), Colleague Commitment to Safety (Cc), Just Culture & Reporting (Jc).
The number of survey items for the seven variables explaining safety behavior and the correlation coefficients for safety behavior are presented in Table 1. The safety behavior questionnaire consists of six items.
| nqs | rsc | p-value | |
|---|---|---|---|
| Ci | 5 | 0.285 | <0.001 |
| Se | 5 | 0.323 | |
| S | 5 | 0.307 | |
| Qa | 5 | 0.444 | |
| Sm | 5 | 0.358 | |
| Cc | 5 | 0.348 | |
| Jc | 5 | 0.438 |
In Table 1, nqs and rsc respectively represent the number of survey items and Spearman’s correlation coefficient (Chrisensen, 2019).
An analysis was conducted to investigate whether there are differences in the perception of safety behavior among flight crew members based on the company of employment or the flight hours of pilots. Table 2 presents the results of comparing the two groups under the assumption of homoscedasticity (t-value=0.343). In Table 2, µ and s represent the mean and standard deviation, respectively (Kim and Choi, 2002).
The average perception values of safety behavior among crew members working for major airlines () in Table 2 were higher than those of crew members employed by low-cost carriers (). However, statistically significant differences could not be identified.
When comparing differences among three or more groups, the results of the analysis of variance indicated a statistically significant difference in the perception of safety behavior among crew members based on flight hours (F-value= 3.145). Table 3 demonstrates that the perception of crew members with flight hours exceeding 10,000 () is higher than those with flight hours of 3,000 or less () and those with moderate flight hours () (Christensen, 2015, Kim and Choi, 2002).
| n | µ | s | p-value | |
|---|---|---|---|---|
| 96 | 3.677 | 0.413 | 0.045 | |
| 111 | 3.631 | 0.452 | ||
| 63 | 3.797 | 0.381 |
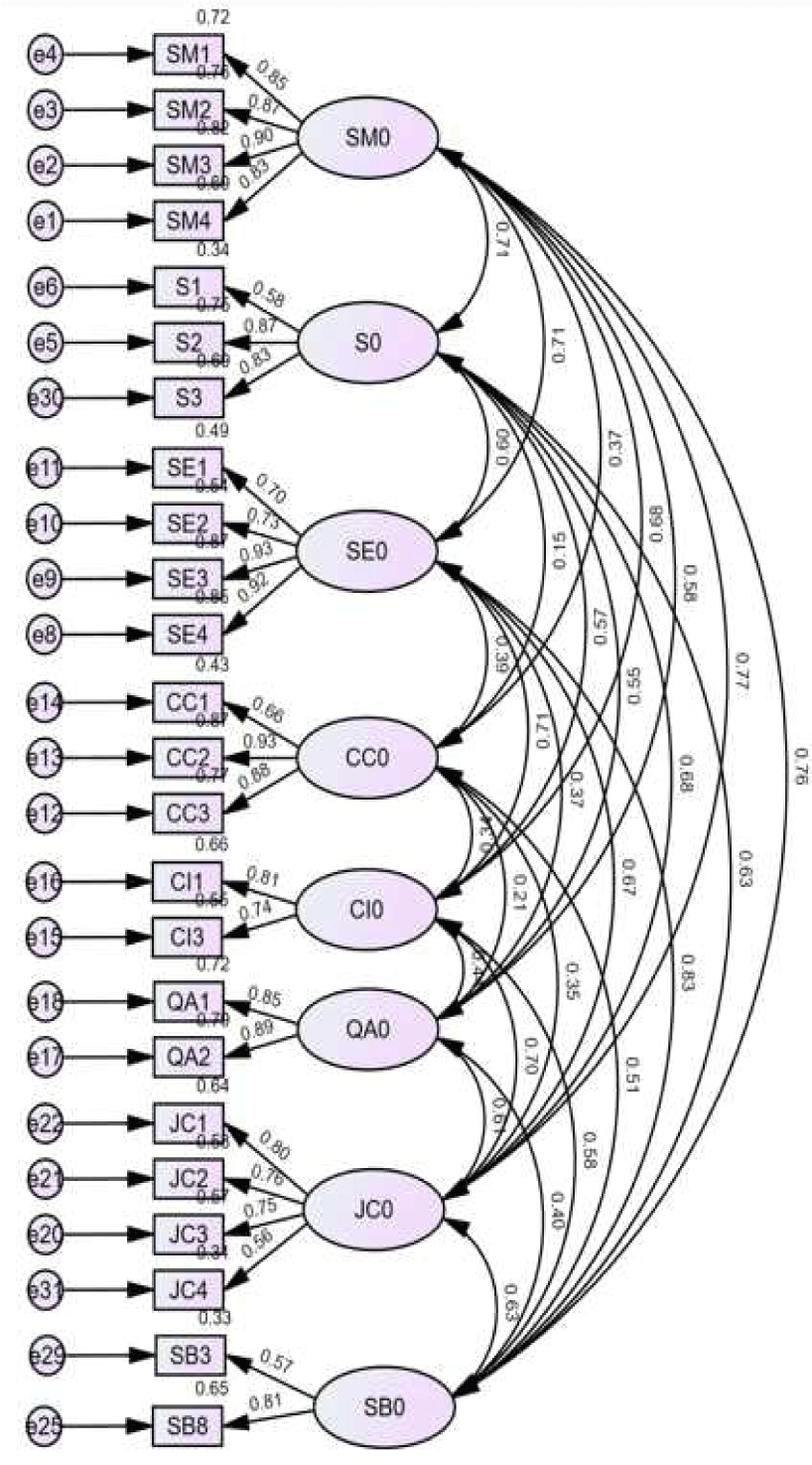
In this study, a confirmatory factor analysis was conducted on the structural equation of flight crew’s safety behavior, involving eight latent variables: Managerial Safety Performance, Organizational Support Perception, Personnel and Equipment, Colleague’s Safety Performance, Cooperation and Involvement, Operational Quality Assurance, Fairness and Voluntary Reporting, and Safety Behavior. The results shown as Fig. 1 revealed that the paths leading to the measurement variables were all statistically significant at a significance level of 0.001. Therefore, the goodness of fit for the structural equation model (SEM) was deemed excellent.
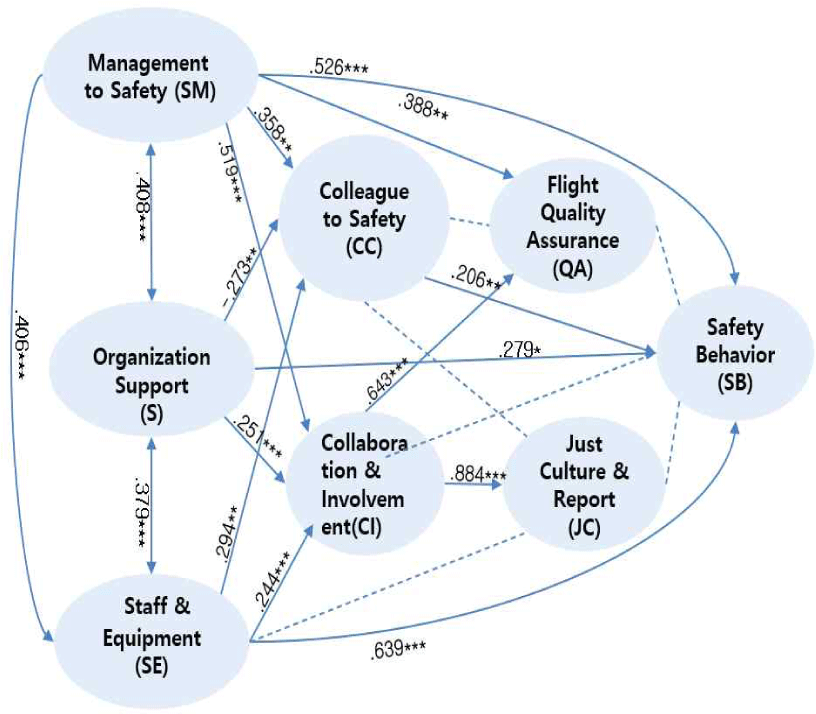
Refers to Fig. 2, to examine the causal relationships among the key variables, we constructed a structural equation model with eight latent variables and observed variables as targets for path analysis, as presented below.
Each path’s significance probability less than 0.05 (*p<0.05, **p<0.01, ***p<0.001) indicates a significant impact, while otherwise, it is considered insignificant. As a result, Collaboration & Involvement, Flight Quality Assurance, and Just Culture & Reporting were analyzed as not significantly influencing Safety Behavior.
Ⅲ. Fuzzy Statistical Analysis for Safety Behavior
In this study, the measurement variables influencing pilots’ safety behavior were investigated using a 5-point Likert scale. However, for flight crew members in the expert group with excellent intellectual abilities, a single-item requiring subjective responses might be more efficient than a questionnaire with multiple items.
As mentioned in Section 2.2 of the SEM, the results of confirmatory factor analysis indicated excellent model fit. However, in path analysis, Collaboration & Involvement, Flight Quality Assurance, and Just Culture & Reporting were found not to have a significant impact on Safety Behavior. To understand the causes of this inconsistency, Fuzzy Statistical Analysis was applied (Zaddeh, 1965, Renato et al., 2006).
In this study, the values of the necessary variables were estimated by selecting the closed interval, which is a subset of the entire set, and recording the values within the selected interval.
In this study, a questionnaire with the content shown in Table 4 was utilized to investigate the subjective perception of safety behavior among flight crew members.
| Statement | Interval | Choose | Score |
|---|---|---|---|
| Strongly disagree | [50,60) | ||
| Disagree | [60,70) | ||
| Neutral | [70,80) | ||
| Agree | [80,90) | a | 86 |
| Strongly agree | [90,100) |
The value measured through the two steps, as shown in the Table 4, were expressed as fuzzy numbers. The membership function µA(X) of the LR fuzzy number A=(a,la,ra)LR with center ‘a’ and left and right spreads la and ra is defined as follows :
Here, LA (RA) are monotonically increasing (decreasing) functions, satisfying LA(0)=RA(0)=1 and LA(1)=RA(1)=1. Additionally, symmetric fuzzy numbers, where the left and right widths are equal, are expressed as A=(a,as)LR. When the membership functions are LA(x)=RA(x)=1–x, it is referred to as a triangular fuzzy number and denoted as A=(a,la,ra)T. The a-level set of the LR fuzzy number A is A(α)=x:µA(x)≥a=[la(α),ra(α)], where the interval endpoints are la(α)=a–laLA-1(α) and ra(α)=a–raRA-1(α) (Dubios and Prade, 1979; Kaufmann and Gupta, 1991).
Using flight crew members’ responses from a subjective questionnaire similar to Table 4, safety behavior and other variables were measured using fuzzy numbers. The variables essential for flight crew members’ safety behavior in Table 5 were represented as symmetrical triangular fuzzy numbers A=(a,sa)T through the following method (Serge et al., 2013; Gerami and Fayek, 2019; Lee and Choi, 2019).
How to get triangular fuzzy number for Sb
Step 1. Divide the universal set () into closed intervals [li,ri](i=1,…,p).
Step 2. Record the values (a) belonging to the selected closed interval [lk,rk].
Step 3. Determination of spread (Sa) of fuzzy number such that Sa=Min|a–lk|,|a–rk|.
The existing research on flight crew members’ safety behavior has primarily employed a 5-point scale questionnaire. In order to analyze the correlation between the results of the conventional 5-point scale questionnaire and the subjectively perceived understanding of flight crew members surveyed with a single item, correlation analysis was conducted.
Table 6 shows the correlation coefficients between the 5-point scale survey and variables measured using fuzzy numbers.
| 1 | 2 | … | p-value | |
|---|---|---|---|---|
| 3.69 | 0.426 | 0.405 | <0.001 | |
| 79.1 | 11.4 |
According to Table 6, there is a statistically significant correlation between the perception of flight crew members measured using a 5-point scale and the perception obtained through a single-item inquiry about subjective thoughts. The potential differences in safety behavior based on the employing airline and flight hours, as analyzed earlier in Section 2.1, were also compared though subjective inquiries.
Table 7 illustrates that the perception of safety behavior among flight crew members from a major airline is higher than that of those from a low-cost airline. The Mann-Whitney test indicates a lack of concordance in the medians of the two groups (13,14). This result diverges from the outcomes obtained using the 5-point scale (refers to Table 2).
| Median | Statistics U | p-value | |
|---|---|---|---|
| 81.0 | 5863 | <0.001 | |
| 79.0 |
To investigate differences in flight crew members’ perceptions based on flight hours, the Kruskal–Wallis test was conducted. In Table 8, Sb(0) and x2 represent the 0-level set and the statistics of the Kruskal–Wallistest, respectively (13,14). Table 8 indicates that there is no statistically significant difference in perception based on flight hours. This finding does not align with the results obtained using the survey instrument (refers to Table 3).
| Sb(0) | Median | x 2 | p-value | |
|---|---|---|---|---|
| [77.5,82.5] | 80.0 | 0.308 | 0.857 | |
| [77.5,82.5] | 80.0 | |||
| [78,82.5] | 80.0 |
Regression analysis, widely applied in statistics, is a method for estimating a statistical model for the response variable (yi) and the explanatory variables based on a finite number
The statistical model is represented as
In classical statistical models, explanatory variables with correlations among the mare typically excluded. Therefore, there are instances where variables essential for the actual environment or the researcher’s design are not included in the regression model.
In Section 2.2, there were originally seven variables identified as influencing safety behavior. However, the path analysis revealed that only four variables, namely Management Commitment to Safety, Perceived Organizational Support, Staff and Equipment, and Colleague Commitment to Safety were found to influence safety behavior. Additionally, the stepwise variable selection method for selecting variables influencing the response variable chose Management Commitment to Safety, Perceived Organizational Support, Staff and Equipment, Colleague Commitment to Safety and Flight Quality Assurance as explanatory variables.
Both path analysis and S Flight Quality Assurance VSM limits the variables influencing safety behavior, identifiedby experts, in the regression model. This approach also partially reflects the results of Structural Equation Modeling. To overcome such limitations, a fuzzy regression model is necessary (Jung et al., 2015, Li at el., 2023).
In 1982, Tanaka applied fuzzy sets proposed by Zadehto regression models, leading to wide spread applications of fuzzy regression models in various fields. In this study, a statistical model for safety behavioris estimated using the explanatory variables
incorporating expert opinions, prior research, and SEM results. To estimate fuzzy regression model
a thre-step procedure is employed, where E=(0,le,re)T represents the fuzzy error.
Step 1 : Calculate Center of 0-level Set.
The center CA of the 0-level set of the fuzzy number A=(0,la,ra) is defined as . Compute the centers for the response variables CSb(j) and explanatory variables Cci(j), CJc(j).
Step 2 : Estimate the Regression Model of Center.
Estimate the regression model of the center for the response variable CSb(j) and the center set of explanatory variables
using the Lasso method (Gholamreza and Mohammad, 2019). The Lasso method minimizes the objective function,
to estimate the regression coefficients, where
and 0<α<1. In this study, we obtain estimates for specific values of αi. Subsequently, the mean for the set αi (i=1,⋯,p) is computed using the Lasso estimation, given by .
Step 3 : Estimate Fuzzy Error E.
Estimate the left spread and right spread of the fuzzy error using the least absolute deviation method. Utilize the left endpoint (lep (j)) and right endpoint (reN (j)) of variables with positive and negative estimated regression coefficients from Step 2, respectively, to determine the left endpoint (leSb (j)) of the response variable.
In the other words, the estimate is obtained by minimizing the expression
Here, and . A similar approach is employed to estimate .
Utilizing the three-step method described above, we estimate the regression model for safety behavior as follows :
In this study, the Lasso regression method was employed in Step 2. The Lasso method, utilizing the L1-norm, estimates regression coefficients for less informative variables to be close to zero, thus diminishing the influence of explanatory variables. In this research, the Lasso method was employed to identify variables with minimal impact on safety behavior. In Step 3, the L1-norm |•| was used to estimate the spread of fuzzy errors. This approach is considered efficient as it is less sensitive to outliers compared to using the L2-norm (•)2 (Choi and Buckley, 2008; Choi and Yoon, 2010; Lee et al., 2021).
The data provided in Table 5 and the results estimated using the Lasso regression method are presented in Table 9.
The fuzzy error presented in Step 3 can be estimated as = 0.4 using lep (j) and. Therefore, the fuzzy regression model for safety behavior can be estimated as:
Commentary: Among the variables influencing the safety behavior of domestic flight crews in South Korea, most of them were found to have a positive and significant impact. However, fairness and voluntary reporting showed a negative impact.
This indicates that flight crews perceive the airline’s reward and penalty system as unfair, leading to a reluctance to make normal voluntary reports.
Table 7 shows differences in flight crews’ subjective perceptions of safety behavior based on the airline they work for. The fuzzy regression models for safety behavior estimated using Steps 1 to 3 for flight crews working in a major airline () and a low-cost airline () are as follows :
Commentary: Flight crews working for low-cost airlines showed a relatively significant perception that the reward and penalty system is unfair compared to flight crews in major airlines.
Table 3 illustrates differences in safety behavior perceptions based on flight experience. The fuzzy regression model for safety behavior estimated using the methods presented in this paper, with a focus on flight hours, is as follows.
The perception () of flight crews with flight hours between 3,000 and 10,000 hours, was positively influenced by all explanatory variables. This indicates a difference between flight crews with less than 3,000 hours () and those with 10,000 hours or more ().
Commentary: Flight crews with lower experience levels face difficulties in voluntary cooperation and participation in the cockpit compared to their more experienced counterparts, stemming from their lack of flight experience.
Moreover, highly experienced flight crew members demonstrate a relatively lower perception of a fair-culture. This indicates that, in comparison to their efforts for safe flight, the compensation is not adequately administered.
Ⅳ. Conclusion
This study conducted a statistical analysis of flight crews’ safety behavior, affecting aviation accidents, yielding significant research findings as follows :
Firstly, in Crisp analysis, the goodness of fit of SEM for each variable was outstanding, but Path Analysis indicated that Collaboration & Involvement, Flight Quality Assurance, Just Culture & Reporting were not significant for. However, in the Fuzzy regression model, the impact of Collaboration & Involvement, Flight Quality Assurance, Just Culture & Reporting on could be analyzed.
Secondly, in the Fuzzy regression model analysis, it was observed that in the case of, flight crew members from low-cost carriers had a relatively unfair influence, leading to a negative impact on safety behavior.
Thirdly, according to the Fuzzy regression model analysis based on flight experience, low-experience flight crew members demonstrated difficulties in voluntary cooperation and participation in the cockpit due to lack of experience.
Lastly, highly experienced flight crew members indicated a negative impact on safety behavior due to inadequate compensation compared to their efforts for safe flight.
The implications of this study lie in the application of both the conventional 5-point scale survey method and fuzzy theory in the statistical analysis of flight crew members’ safety behavior. The subjective responses of flight crew members, who are a group of experts with excellent intellectual abilities, were transformed into fuzzy numbers. The estimated fuzzy regression model enabled the explanation of the impact of explanatory variables on safety behavior.
Future research may explore broader applications of fuzzy sets, which can represent data with uncertainty, in the field of flight safety.